Matrix calculus

  1. Given a matrix A of size m \times n and a vector x of size n \times 1, compute the gradient of the function f(x) = \text{tr}(A^T A x x^T) with respect to x.

  2. Find the gradient \nabla f(x) and hessian f''(x), if f(x) = \dfrac{1}{2} \Vert Ax - b\Vert^2_2.

  3. Find the gradient \nabla f(x) and hessian f''(x), if f(x) = \frac1m \sum\limits_{i=1}^m \log \left( 1 + \exp(a_i^{T}x) \right) + \frac{\mu}{2}\Vert x\Vert _2^2, \; a_i, x \in \mathbb R^n, \; \mu>0

  4. Compute the gradient \nabla_A f(A) of the trace of the matrix exponential function f(A) = \text{tr}(e^A) with respect to A. Hint: hint: Use the definition of the matrix exponential. Use the definition of the differential df = f(A + dA) - f(A) + o(\Vert dA \Vert) with the limit \Vert dA \Vert \to 0.

  5. Find the gradient \nabla f(x) and hessian f''(x), if f(x) = \frac{1}{2}\Vert A - xx^T\Vert^2_F, A \in \mathbb{S}^n

  6. Calculate the first and the second derivative of the following function f : S \to \mathbb{R}

    f(t) = \text{det}(A − tI_n),

    where A \in \mathbb{R}^{n \times n}, S := \{t \in \mathbb{R} : \text{det}(A − tI_n) \neq 0\}.

  7. Find the gradient \nabla f(X), if f(X) = \text{tr}\left( AX^2BX^{-\top} \right).

Automatic differentiation and jax

You can use any automatic differentiation framework in this section (Jax, PyTorch, Autograd etc.)

  1. You will work with the following function for this exercise, f(x,y)=e^{−\left(sin(x)−cos(y)\right)^2}
    Draw the computational graph for the function. Note, that it should contain only primitive operations - you need to do it automatically - jax example, PyTorch example - you can google/find your way to visualize it.

  2. Compare analytic and autograd (with any framework) approach for the calculation of the gradient of:
    f(A) = \text{tr}(e^A)

  3. We can use automatic differentiation not only to calculate necessary gradients but also for tuning hyperparameters of the algorithm like learning rate in gradient descent (with gradient descent 🤯). Suppose, we have the following function f(x) = \frac{1}{2}\Vert x\Vert^2, select a random point x_0 \in \mathbb{B}^{1000} = \{0 \leq x_i \leq 1 \mid \forall i\}. Consider 10 steps of the gradient descent starting from the point x_0: x_{k+1} = x_k - \alpha_k \nabla f(x_k) Your goal in this problem is to write the function, that takes 10 scalar values \alpha_i and return the result of the gradient descent on function L = f(x_{10}). And optimize this function using gradient descent on \alpha \in \mathbb{R}^{10}. Suppose that each of 10 components of \alpha is uniformly distributed on [0; 0.1]. \alpha_{k+1} = \alpha_k - \beta \frac{\partial L}{\partial \alpha} Choose any constant \beta and the number of steps you need. Describe the obtained results. How would you understand, that the obtained schedule (\alpha \in \mathbb{R}^{10}) becomes better than it was at the start? How do you check numerically local optimality in this problem?

  4. Compare analytic and autograd (with any framework) approach for the gradient of:
    f(X) = - \log \det X

  5. Compare analytic and autograd (with any framework) approach for the gradient and hessian of:
    f(x) = x^\top x x^\top x

Convex sets

  1. Show, that if S \subseteq \mathbb{R}^n is convex set, then its interior \mathbf{int } S and closure \bar{S} are also convex sets.
  2. Show, that \mathbf{conv}\{xx^\top: x \in \mathbb{R}^n, \Vert x\Vert = 1\} = \{A \in \mathbb{S}^n_+: \text{tr}(A) = 1\}.
  3. Let K \subseteq \mathbb{R}^n_+ is a cone. Prove that it is convex if and only if a set of \{x \in K \mid \sum\limits_{i=1}^n x_i = 1 \} is convex.
  4. Prove that the set of \{x \in \mathbb{R}^2 \mid e^{x_1}\le x_2\} is convex.
  5. Show that the set of directions of the non-strict local descending of the differentiable function in a point is a convex cone. (Previously, the question contained a typo “strict local descending”)
  6. Is the following set convex S = \left\{ a \in \mathbb{R}^k \mid p(0) = 1, \vert p(t) \vert\leq 1 \text{ for } \alpha\leq t \leq \beta\right\}, where p(t) = a_1 + a_2 t + \ldots + a_k t^{k-1} \;?

Convex functions

  1. Consider the function f(x) = x^d, where x \in \mathbb{R}_{+}. Fill the following table with ✅ or ❎. Explain your answers

    d Convex Concave Strictly Convex \mu-strongly convex
    -2, x \in \mathbb{R}_{++}
    -1, x \in \mathbb{R}_{++}
    0
    0.5
    1
    \in (1; 2)
    2
    > 2

  2. Prove that the entropy function, defined as

    f(x) = -\sum_{i=1}^n x_i \log(x_i),

    with \text{dom}(f) = \{x \in \R^n_{++} : \sum_{i=1}^n x_i = 1\}, is strictly concave.

  3. Show, that the function f: \mathbb{R}^n_{++} \to \mathbb{R} is convex if f(x) = - \prod\limits_{i=1}^n x_i^{\alpha_i} if \mathbf{1}^T \alpha = 1, \alpha \succeq 0.

  4. Show that the maximum of a convex function f over the polyhedron P = \text{conv}\{v_1, \ldots, v_k\} is achieved at one of its vertices, i.e.,

    \sup_{x \in P} f(x) = \max_{i=1, \ldots, k} f(v_i).

    A stronger statement is: the maximum of a convex function over a closed bounded convex set is achieved at an extreme point, i.e., a point in the set that is not a convex combination of any other points in the set. (you do not have to prove it). Hint: Assume the statement is false, and use Jensen’s inequality.

  5. Show, that the two definitions of \mu-strongly convex functions are equivalent:

    1. f(x) is \mu-strongly convex \iff for any x_1, x_2 \in S and 0 \le \lambda \le 1 for some \mu > 0:

      f(\lambda x_1 + (1 - \lambda)x_2) \le \lambda f(x_1) + (1 - \lambda)f(x_2) - \frac{\mu}{2} \lambda (1 - \lambda)\|x_1 - x_2\|^2

    2. f(x) is \mu-strongly convex \iff if there exists \mu>0 such that the function f(x) - \dfrac{\mu}{2}\Vert x\Vert^2 is convex.

Conjugate sets

  1. Let \mathbb{A}_n be the set of all n dimensional antisymmetric matrices (s.t. X^T = - X). Show that \left( \mathbb{A}_n\right)^* = \mathbb{S}_n.

  2. Find the sets S^{*}, S^{**}, S^{***}, if

    S = \{ x \in \mathbb{R}^2 \mid x_1 + x_2 \ge 0, \;\; -\dfrac12x_1 + x_2 \ge 0, \;\; 2x_1 + x_2 \ge -1 \;\; -2x_1 + x_2 \ge -3\}

  3. Prove, that B_p and B_{p_*} are inter-conjugate, i.e. (B_p)^* = B_{p_*}, (B_{p_*})^* = B_p, where B_p is the unit ball (w.r.t. p - norm) and p, p_* are conjugated, i.e. p^{-1} + p^{-1}_* = 1. You can assume, that p_* = \infty if p = 1 and vice versa.

Conjugate functions

  1. Find f^*(y), if f(x) = \vert 2x \vert

  2. Prove, that if f(x) = \inf\limits_{u+v = x} (g(u) + h(v)), then f^*(y) = g^*(y) + h^*(y).

  3. Find f^*(y), if f(x) = \log \left( \sum\limits_{i=1}^n e^{x_i} \right)

  4. Prove, that if f(x) = g(Ax), then f^*(y) = g^*(A^{-\top}y)

  5. Find f^*(Y), if f(X) = - \ln \det X, X \in \mathbb{S}^n_{++}

  6. The scalar Huber function is defined as

    f_{\text{hub}}(x) = \begin{cases} \frac{1}{2} x^2 & \text{if } |x| \leq 1 \\ |x| - \frac{1}{2} & \text{if } |x| > 1 \end{cases}

    Scalar case

    This convex function arises in various applications, notably in robust estimation. This problem explores the generalizations of the Huber function to \mathbb{R}^n. A straightforward extension to \mathbb{R}^n is expressed as f_{\text{hub}}(x_1) + \ldots + f_{\text{hub}}(x_n), yet this formulation is not circularly symmetric, that is, it’s not invariant under the transformation of x by an orthogonal matrix. A circularly symmetric extension to \mathbb{R}^n is given by

    f_{\text{cshub}}(x) = f_{\text{hub}}(\Vert x\Vert )= \begin{cases} \frac{1}{2} \Vert x\Vert_2 ^2 & \text{if } \Vert x\Vert_2 \leq 1 \\ \Vert x\Vert_2 - \frac{1}{2} & \text{if } \Vert x\Vert_2 > 1 \end{cases}

    where the subscript denotes “circularly symmetric Huber function”. Show, that f_{\text{cshub}} is convex. Find the conjugate function f^*(y).

Subgradient and subdifferential

  1. Find \partial f(x), if f(x) = \text{Parametric ReLU}(x) = \begin{cases} x & \text{if } x > 0, \\ ax & \text{otherwise}. \end{cases}
  2. Prove, that x_0 - is the minimum point of a function f(x) if and only if 0 \in \partial f(x_0).
  3. Find \partial f(x), if f(x) = \Vert Ax - b\Vert _1.
  4. Find \partial f(x), if f(x) = e^{\Vert x\Vert}.
  5. Find \partial f(x), if f(x) = \frac12 \Vert Ax - b\Vert _2^2 + \lambda \Vert x\Vert_1, \quad \lambda > 0.
  6. Let S \subseteq \mathbb{R}^n be a convex set. We will call a normal cone of the set S at a point x the following set: N_S(x) = \left\{c \in \mathbb{R}^n : \langle c, y-x\rangle \leq 0 \quad \forall y \in S\right\}

    1. Draw a normal cone for a set at the points A, B, C, D, E, F on the figure below:

      Draw a normal cone for the set S in these points

    2. Show, that N_S(x) = \{0\} \quad \forall x \in \mathbf{ri }(S).

    3. Show, that the subdifferential \partial I_S(x) = N_S(x) if I_S(x) is the indicator function, i.e.  I_S(x) = \begin{cases}0,\text{if } x \in S\\ \infty, \text{otherwise}\end{cases}

KKT and duality

In this section, you can consider either the arbitrary norm or the Euclidian norm if nothing else is specified.

  1. Toy example \begin{split} & x^2 + 1 \to \min\limits_{x \in \mathbb{R} }\\ \text{s.t. } & (x-2)(x-4) \leq 0 \end{split}

    1. Give the feasible set, the optimal value, and the optimal solution.
    2. Plot the objective x^2 +1 versus x. On the same plot, show the feasible set, optimal point, and value, and plot the Lagrangian L(x,\mu) versus x for a few positive values of \mu. Verify the lower bound property (p^* \geq \inf_x L(x, \mu)for \mu \geq 0). Derive and sketch the Lagrange dual function g.
    3. State the dual problem, and verify that it is a concave maximization problem. Find the dual optimal value and dual optimal solution \mu^*. Does strong duality hold?
    4. Let p^*(u) denote the optimal value of the problem

    \begin{split} & x^2 + 1 \to \min\limits_{x \in \mathbb{R} }\\ \text{s.t. } & (x-2)(x-4) \leq u \end{split}

    as a function of the parameter u. Plot p^*(u). Verify that \dfrac{dp^*(0)}{du} = -\mu^*

  2. Derive the dual problem for the Ridge regression problem with A \in \mathbb{R}^{m \times n}, b \in \mathbb{R}^m, \lambda > 0:

    \begin{split} \dfrac{1}{2}\|y-b\|^2 + \dfrac{\lambda}{2}\|x\|^2 &\to \min\limits_{x \in \mathbb{R}^n, y \in \mathbb{R}^m }\\ \text{s.t. } & y = Ax \end{split}

  3. Derive the dual problem for the support vector machine problem with A \in \mathbb{R}^{m \times n}, \mathbf{1} \in \mathbb{R}^m \in \mathbb{R}^m, \lambda > 0:

    \begin{split} \langle \mathbf{1}, t\rangle + \dfrac{\lambda}{2}\|x\|^2 &\to \min\limits_{x \in \mathbb{R}^n, t \in \mathbb{R}^m }\\ \text{s.t. } & Ax \succeq \mathbf{1} - t \\ & t \succeq 0 \end{split}

  4. Give an explicit solution to the following LP.

    \begin{split} & c^\top x \to \min\limits_{x \in \mathbb{R}^n }\\ \text{s.t. } & 1^\top x = 1, \\ & x \succeq 0 \end{split}

    This problem can be considered the simplest portfolio optimization problem.

  5. Show, that the following problem has a unique solution and find it:

    \begin{split} & \langle C^{-1}, X\rangle - \log \det X \to \min\limits_{x \in \mathbb{R}^{n \times n} }\\ \text{s.t. } & \langle Xa, a\rangle \leq 1, \end{split}

    where C \in \mathbb{S}^n_{++}, a \in \mathbb{R}^n \neq 0. The answer should not involve inversion of the matrix C.

  6. Give an explicit solution to the following QP.

    \begin{split} & c^\top x \to \min\limits_{x \in \mathbb{R}^n }\\ \text{s.t. } & (x - x_c)^\top A (x - x_c) \leq 1, \end{split}

    where A \in \mathbb{S}^n_{++}, c \neq 0, x_c \in \mathbb{R}^n.

  7. Consider the equality-constrained least-squares problem

    \begin{split} & \|Ax - b\|_2^2 \to \min\limits_{x \in \mathbb{R}^n }\\ \text{s.t. } & Cx = d, \end{split}

    where A \in \mathbb{R}^{m \times n} with \mathbf{rank }A = n, and C \in \mathbb{R}^{k \times n} with \mathbf{rank }C = k. Give the KKT conditions, and derive expressions for the primal solution x^* and the dual solution \lambda^*.

  8. Derive the KKT conditions for the problem

    \begin{split} & \mathbf{tr \;}X - \log\text{det }X \to \min\limits_{X \in \mathbb{S}^n_{++} }\\ \text{s.t. } & Xs = y, \end{split}

    where y \in \mathbb{R}^n and s \in \mathbb{R}^n are given with y^\top s = 1. Verify that the optimal solution is given by

    X^* = I + yy^\top - \dfrac{1}{s^\top s}ss^\top

  9. Supporting hyperplane interpretation of KKT conditions. Consider a convex problem with no equality constraints

    \begin{split} & f_0(x) \to \min\limits_{x \in \mathbb{R}^n }\\ \text{s.t. } & f_i(x) \leq 0, \quad i = [1,m] \end{split}

    Assume, that \exists x^* \in \mathbb{R}^n, \mu^* \in \mathbb{R}^m satisfy the KKT conditions

    \begin{split} & \nabla_x L (x^*, \mu^*) = \nabla f_0(x^*) + \sum\limits_{i=1}^m\mu_i^*\nabla f_i(x^*) = 0 \\ & \mu^*_i \geq 0, \quad i = [1,m] \\ & \mu^*_i f_i(x^*) = 0, \quad i = [1,m]\\ & f_i(x^*) \leq 0, \quad i = [1,m] \end{split}

    Show that

    \nabla f_0(x^*)^\top (x - x^*) \geq 0

    for all feasible x. In other words, the KKT conditions imply the simple optimality criterion or \nabla f_0(x^*) defines a supporting hyperplane to the feasible set at x^*.

  10. Fenchel + Lagrange = ♥. Express the dual problem of

    \begin{split} & c^\top x\to \min\limits_{x \in \mathbb{R}^n }\\ \text{s.t. } & f(x) \leq 0 \end{split}

    with c \neq 0, in terms of the conjugate function f^*. Explain why the problem you give is convex. We do not assume f is convex.

  11. A penalty method for equality constraints. We consider the problem of minimization

    \begin{split} & f_0(x) \to \min\limits_{x \in \mathbb{R}^{n} }\\ \text{s.t. } & Ax = b, \end{split}

    where $f_0(x): ^n $ is convex and differentiable, and A \in \mathbb{R}^{m \times n} with \mathbf{rank }A = m. In a quadratic penalty method, we form an auxiliary function

    \phi(x) = f_0(x) + \alpha \|Ax - b\|_2^2,

    where \alpha > 0 is a parameter. This auxiliary function consists of the objective plus the penalty term \alpha \Vert Ax - b\Vert_2^2. The idea is that a minimizer of the auxiliary function, \tilde{x}, should be an approximate solution to the original problem. Intuition suggests that the larger the penalty weight \alpha, the better the approximation \tilde{x} to a solution of the original problem. Suppose \tilde{x} is a minimizer of \phi(x). Show how to find, from \tilde{x}, a dual feasible point for the original problem. Find the corresponding lower bound on the optimal value of the original problem.

  12. Analytic centering. Derive a dual problem for

    -\sum_{i=1}^m \log (b_i - a_i^\top x) \to \min\limits_{x \in \mathbb{R}^{n} }

    with domain \{x \mid a^\top_i x < b_i , i = [1,m]\}.

    First introduce new variables y_i and equality constraints y_i = b_i − a^\top_i x. (The solution to this problem is called the analytic center of the linear inequalities a^\top_i x \leq b_i ,i = [1,m]. Analytic centers have geometric applications, and play an important role in barrier methods.)

Linear programming

  1. 📱🎧💻 Covers manufacturing. Lyzard Corp is producing covers for the following products:

    • 📱 phones
    • 🎧 headphones
    • 💻 laptops

    The company’s production facilities are such that if we devote the entire production to headphone covers, we can produce 5000 of them in one day. If we devote the entire production to phone covers or laptop covers, we can produce 4000 or 2000 of them in one day.

    The production schedule is one week (6 working days), and the week’s production must be stored before distribution. Storing 1000 headphone covers (packaging included) takes up 30 cubic feet of space. Storing 1000 phone covers (packaging included) takes up 50 cubic feet of space, and storing 1000 laptop covers (packaging included) takes up 220 cubic feet of space. The total storage space available is 1500 cubic feet.

    Due to commercial agreements with Lyzard Corp has to deliver at least 4500 headphone covers and 4000 laptop covers per week to strengthen the product’s diffusion.

    The marketing department estimates that the weekly demand for headphones covers, phone, and laptop covers does not exceed 10000 14000, and 7000 units, therefore the company does not want to produce more than these amounts for headphones, phone, and laptop covers.

    Finally, the net profit per headphone cover, phone cover, and laptop cover are $5, $7, and $12, respectively.

    The aim is to determine a weekly production schedule that maximizes the total net profit.

    1. Write a Linear Programming formulation for the problem. Use the following variables:

      • y_1 = number of headphones covers produced over the week,
      • y_2 = number of phone covers produced over the week,
      • y_3 = number of laptop covers produced over the week.

    2. Find the solution to the problem using PyOMO

      !pip install pyomo
! sudo apt-get install glpk-utils --quiet  # GLPK
! sudo apt-get install coinor-cbc --quiet  # CoinOR

    3. Perform the sensitivity analysis. Which constraint could be relaxed to increase the profit the most? Prove it numerically.

  2. Prove the optimality of the solution

    x = \left(\frac{7}{3} , 0, \frac{1}{3}\right)^T

    to the following linear programming problem:

    \begin{split} & 9x_1 + 3x_2 + 7x_3 \to \max\limits_{x \in \mathbb{R}^3 }\\ \text{s.t. } & 2x_1 + x_2 + 3x_3 \leq 6 \\ & 5x_1 + 4x_2 + x_3 \leq 12 \\ & 3x_3 \leq 1,\\ & x_1, x_2, x_3 \geq 0 \end{split}

    but you cannot use any numerical algorithm here.

  3. Transform the following linear program into an equivalent linear program in the standard form \left(c^\top x \to \min\limits_{x\in \mathbb{R}^n} : Ax = b,x ≥ 0\right):

    \begin{split} & x_1−x_2 \to \min\limits_{x \in \mathbb{R}^2 }\\ \text{s.t. } & 2x_1 + x_2 \geq 3 \\ & 3x_1 − x_2 \leq 7 \\ & x_1 \geq 0 \end{split}

  4. Consider:

    \begin{split} & 4x_1 + 5x_2 + 2x_3 \to \max\limits_{x \in \mathbb{R}^3 }\\ \text{s.t. } & 2x_1 - x_2 + 2x_3 \leq 9 \\ & 3x_1 + 5x_2 + 4x_3 \leq 8 \\ & x_1 + x_2 + 2x_3 \leq 2 \\ & x_1, x_2, x_3 \geq 0, \end{split}

    1. Find an optimal solution to the Linear Programming problem using the simplex method.
    2. Write the dual linear program. Find an optimal dual solution. Do we have strong duality here?

Sequence convergence

  1. Determine the convergence or divergence of a given sequences

    • r_{k} = \frac{1}{\sqrt{k}}.
    • r_{k} = 0.606^k.
    • r_{k} = 0.606^{2^k}.

  2. Determine the convergence or divergence of a given sequence r_k =\begin{cases} \frac{1}{k}, & \text{if } k\text{ is even} \\ e^{-k}, & \text{if } k\text{ is odd} \end{cases}.

  3. Determine the following sequence \{r_k\} by convergence rate (linear, sublinear, superlinear). In the case of superlinear convergence, additionally, find out whether there is quadratic convergence.

    r_k = \dfrac{1}{k!}

  4. Determine the following sequence \{r_k\} by convergence rate (linear, sublinear, superlinear). In the case of superlinear convergence, additionally find out whether there is quadratic convergence.

    r_k = \dfrac{1}{k^k}

  5. Let \{r_k\} be a sequence of non-negative numbers given as r_{k+1} = Mr_k^2, where M > 0, r_0 \geq 0. Establish a necessary and sufficient condition on M and r_0 under which the sequence r_k will converge to zero. What is the rate of convergence?

Zero-order methods

  1. Solve approximately the Travelling Salesman Problem with any zero-order optimization method.

    Illustration of TSP
    import numpy as np
from scipy.spatial import distance_matrix
import random

def generate_random_symmetric_tsp(num_cities, seed=0):
    np.random.seed(seed)
    points = np.random.rand(num_cities, 2)  # Generate random coordinates
    dist_matrix = distance_matrix(points, points)
    dist_matrix = (dist_matrix + dist_matrix.T) / 2  # Ensure symmetry
    return jnp.array(dist_matrix)  # Convert to JAX array for further processing

# Example usage
num_cities = 10
dist_matrix = generate_random_symmetric_tsp(num_cities)
print(dist_matrix)
    • You can use the genetic algorithm with any significant modification of mutation(5/10)
    • You can use another algorithm (10/10)

  2. In this assignment, we aim to explore and compare the efficacy of traditional and zero-order optimization methods in training a simple neural network. The conventional approach, Stochastic Gradient Descent (SGD), has been widely used due to its efficiency in handling large datasets and its capability to work in a huge-scale setting. This method relies on gradients of the loss function with respect to the network’s parameters. In contrast, zero-order optimization methods, also known as derivative-free methods, optimize without explicit gradient information. These methods are particularly useful for non-differentiable, noisy, or highly complex loss landscapes. The assignment’s objective is to explore such algorithms as Genetic Algorithms, Simulated Annealing, Gradient-free methods, or the Nelder-Mead method for real-world problems.

    Note, that a variety of feed-forward neural networks could be represented as a series of linear transformations, followed by some nonlinear function (say, \text{ReLU }(x)):

    \mathcal{NN}(x) = f_L \circ w_L \circ \ldots \circ f_1 \circ w_1 \circ x,

    where L is the number of layers, f_i - non-linear activation function, w_i = W_i x + b_i - linear layer. We can denote the training data by X and the labels by y. The overall optimization problem here is to train the neural network to approximate the mapping X \to y, i.e. \mathcal{NN}(X) should be as close to y as possible for all data points. We can ensure this by minimizing the loss function, which depends on the neural network parameters:

    \mathcal{L}(\mathcal{NN}(X, W, b), y) \to \min_{W, b}

    Typically, we use a cross-entropy loss function for the classification task. Do not worry if you are not familiar with neural networks or machine learning. Try to focus on the optimization algorithm here. You are provided with an example of this approach in the Colab notebook.

    Comparison of SGD vs Evolutionary strategy for neural network without hidden layer.

    Comparison of SGD vs Evolutionary strategy for neural network with several hidden layers.

    The assignment requires you to implement a chosen zero-order optimization algorithm and compare its performance against SGD in training a predefined simple neural network (you can vary the structure of the network as you want for this problem). The comparison should focus on aspects such as convergence speed, final accuracy, and computational efficiency. Students should provide a name of the chosen zero-order algorithm and implement it in Python. You can use any method you want except the Evolutionary strategy, which is already in the example above.

Gradient Descent

  1. Convergence of Gradient Descent in non-convex smooth case (10 points)

    We will assume nothing about the convexity of f. We will show that gradient descent reaches an \varepsilon-substationary point x, such that \|\nabla f(x)\|_2 \leq \varepsilon, in O(1/\varepsilon^2) iterations. Important note: you may use here Lipschitz parabolic upper bound:

    f(y) \leq f(x) + \nabla f(x)^T (y-x) + \frac{L}{2} \|y-x\|_2^2, \;\;\; \text{for all $x,y$}. \tag{1}

    • Plug in y = x^{k+1} = x^{k} - \alpha \nabla f(x^k), x = x^k to (Equation 1) to show that

      f(x^{k+1}) \leq f(x^k) - \Big (1-\frac{L\alpha}{2} \Big) \alpha \|\nabla f(x^k)\|_2^2.

    • Use \alpha \leq 1/L, and rearrange the previous result, to get

      \|\nabla f(x^k)\|_2^2 \leq \frac{2}{\alpha} \left( f(x^k) - f(x^{k+1}) \right).

    • Sum the previous result over all iterations from 1,\ldots,k+1 to establish

      \sum_{i=0}^k \|\nabla f(x^{i})\|_2^2 \leq \frac{2}{\alpha} ( f(x^{0}) - f^*).

    • Lower bound the sum in the previous result to get

      \min_{i=0,\ldots,k} \|\nabla f(x^{i}) \|_2 \leq \sqrt{\frac{2}{\alpha(k+1)} (f(x^{0}) - f^*)}, which establishes the desired O(1/\varepsilon^2) rate for achieving \varepsilon-substationarity.

  2. How gradient descent convergence depends on the condition number and dimensionality. (20 points)

    Investigate how the number of iterations required for gradient descent to converge depends on the following two parameters: the condition number \kappa \geq 1 of the function being optimized, and the dimensionality n of the space of variables being optimized.

    To do this, for given parameters n and \kappa, randomly generate a quadratic problem of size n with condition number \kappa and run gradient descent on it with some fixed required precision. Measure the number of iterations T(n, \kappa) that the method required for convergence (successful termination based on the stopping criterion).

    Recommendation: The simplest way to generate a random quadratic problem of size n with a given condition number \kappa is as follows. It is convenient to take a diagonal matrix A \in S_{n}^{++} as simply the diagonal matrix A = \text{Diag}(a), whose diagonal elements are randomly generated within [1, \kappa], and where \min(a) = 1, \max(a) = \kappa. As the vector b \in \mathbb{R}^n, you can take a vector with random elements. Diagonal matrices are convenient to consider since they can be efficiently processed with even for large values of n.

    Fix a certain value of the dimensionality n. Iterate over different condition numbers \kappa on a grid and plot the dependence of T(n,\kappa) against \kappa. Since the quadratic problem is generated randomly each time, repeat this experiment several times. As a result, for a fixed value of n, you should obtain a whole family of curves showing the dependence of T(n, \kappa) on \kappa. Draw all these curves in the same color for clarity (for example, red).

    Now increase the value of n and repeat the experiment. You should obtain a new family of curves T(n',\kappa) against \kappa. Draw all these curves in the same color but different from the previous one (for example, blue).

    Repeat this procedure several times for other values of n. Eventually, you should have several different families of curves - some red (corresponding to one value of n), some blue (corresponding to another value of n), some green, etc.

    Note that it makes sense to iterate over the values of the dimensionality n on a logarithmic grid (for example, n = 10, n = 100, n = 1000, etc.). Use the following stopping criterion: \|\nabla f(x_k)\|_2^2 \leq \varepsilon \|\nabla f(x_0)\|_2^2 with \varepsilon = 10^{-5}. Select the starting point x_0 = (1, \ldots, 1)^T

    What conclusions can be drawn from the resulting picture?

Subgradient Descent

  1. Subgradient descent convergence with several stepsize strategies. (10 points)

    In this problem you will have to prove the convergence of subgradient descent (x^{k+1} = x^k - \alpha_k g_k) for several stepsize strategies. First prove, that

    \|x^{k+1} - x^*\|_2^2 \leq \|x^{k} - x^*\|_2^2 - 2\alpha_k \left(f(x^k) - f^* \right) + \alpha^2_k \|g_k\|_2^2

    Then, using \|g\|_2 \leq G, \|x^0 - x^*\| \leq R prove, that

    \|x^{k+1} - x^*\|_2^2 \leq R^2 - 2\sum\limits_{i=1}^k\alpha_i \left(f(x^i) - f^* \right) + G^2\sum\limits_{i=1}^k\alpha^2_i

    Then, using f_k^{\text{best}} = \min\limits_{i=1,\ldots,k} f(x^i) prove, that

    f_k^{\text{best}} - f^* \leq \frac{R^2 + G^2\sum\limits_{i=1}^k\alpha^2_i}{2\sum\limits_{i=1}^k\alpha_i}

    After that, finalize the bound for the following stepsize choosing strategies

    • constant step size \alpha_k = \alpha

    • constant step length \alpha_k = \frac{\gamma}{\|g_k\|_2} (so \|x^{k+1} - x^k\|_2 = \gamma)

    • Inverse square root \frac{R}{G\sqrt{k}}

    • Inverse \frac1k

    • Polyak’s step size:

      \alpha_k = \frac{f(x^k) - f^*}{\|g_k\|_2^2}

  2. Subgradient methods for Lasso. (10 points)

    Consider the optimization problem

    \min_{x \in \mathbb{R}^n} f(x) := \frac12 \|Ax - b\|^2 + \lambda \|x\|_1,

    with variables x \in \mathbb{R}^n and problem data A \in \mathbb{R}^{m \times n}, b \in \mathbb{R}^m and \lambda > 0. This model is known as Lasso, or Least Squares with l_1 regularization, which encourages sparsity in the solution via the non-smooth penalty \|x\|_1 := \sum_{j=1}^n |x_j|. In this problem, we will explore various subgradient methods for fitting this model.

    • Derive the subdifferential \partial f(x) of the objective.

    • Find the update rule of the subgradient method and state the computational complexity of applying one update using big O notation in terms of the dimensions.

    • Let n = 1000, m = 200 and \lambda = 0.01. Generate a random matrix A \in \mathbb{R}^{m \times n} with independent Gaussian entries with mean 0 and variance 1/m, and a fixed vector x^* = {\underbrace{[1, \ldots, 1}_{\text{k times}}, \underbrace{0, \ldots, 0]}_{\text{n-k times}}}^T \in \mathbb{R}^n. Let k = 5 and then set b = Ax^*. Implement the subgradient method to minimize f(x), initialized at the all-zeros vector. Try different step size rules, including:

      • constant step size \alpha_k = \alpha

      • constant step length \alpha_k = \frac{\gamma}{\|g_k\|_2} (so \|x^{k+1} - x^k\|_2 = \gamma)

      • Inverse square root \frac{1}{\sqrt{k}}

      • Inverse \frac1k

      • Polyak’s step length with estimated objective value:

        \alpha_k = \frac{f(x_k) - f_k^{\text{best}} + \gamma_k}{\|g_k\|_2^2}, \quad \text{ with} \sum_{k=1}^\infty \gamma_k = \infty, \quad \sum_{k=1}^\infty \gamma_k^2 < \infty

        For example, one can use \gamma_k = \frac{10}{10 + k}. Here f_k^{\text{best}} - \gamma_k serves as estimate of f^*. It is better to take \gamma_k in the same scale as the objective value. One can show, that f_k^{\text{best}} \to f^*.

      Plot objective value versus iteration curves of different step size rules on the same figure.

    • Repeat previous part using a heavy ball term, \beta_k(x^k - x^{k-1}), added to the subgradient. Try different step size rules as in the previous part and tune the heavy ball parameter \beta_k = \beta for faster convergence.

  3. Finding a point in the intersection of convex sets. (20 points)

    Let A \in \mathbb{R}^{n \times n} be a positive definite matrix and let \Sigma be an n \times n diagonal matrix with diagonal entries \sigma_1,...,\sigma_n > 0, and y a given vector in \mathbb{R}^n. Consider the compact convex sets U = \{x \in \mathbb{R}^n \mid \|A^{1/2}(x-y)\|_2 \leq 1\} and V = \{x \in \mathbb{R}^n \mid \|\Sigma x\|_\infty \leq 1\}.

    • Minimize maximum distance from the current point to the convex sets.

      \min_{x\in\mathbb{R}^n} f(x) = \min_{x\in\mathbb{R}^n} \max\{\mathbf{dist}(x, U), \mathbf{dist}(x, V)\}

      propose an algorithm to find a point x \in U \cap V. You can assume that U \cap V is not empty. Your algorithm must be provably converging (although you do not need to prove it and you can simply refer to the lecture slides).

    • Implement your algorithm with the following data: n = 2, y = (3, 2), \sigma_1 = 0.5, \sigma_2 = 1,

      A = \begin{bmatrix} 1 & 0 \\ -1 & 1 \end{bmatrix},

      and x = (2, 1). Plot the objective value of your optimization problem versus the number of iterations.

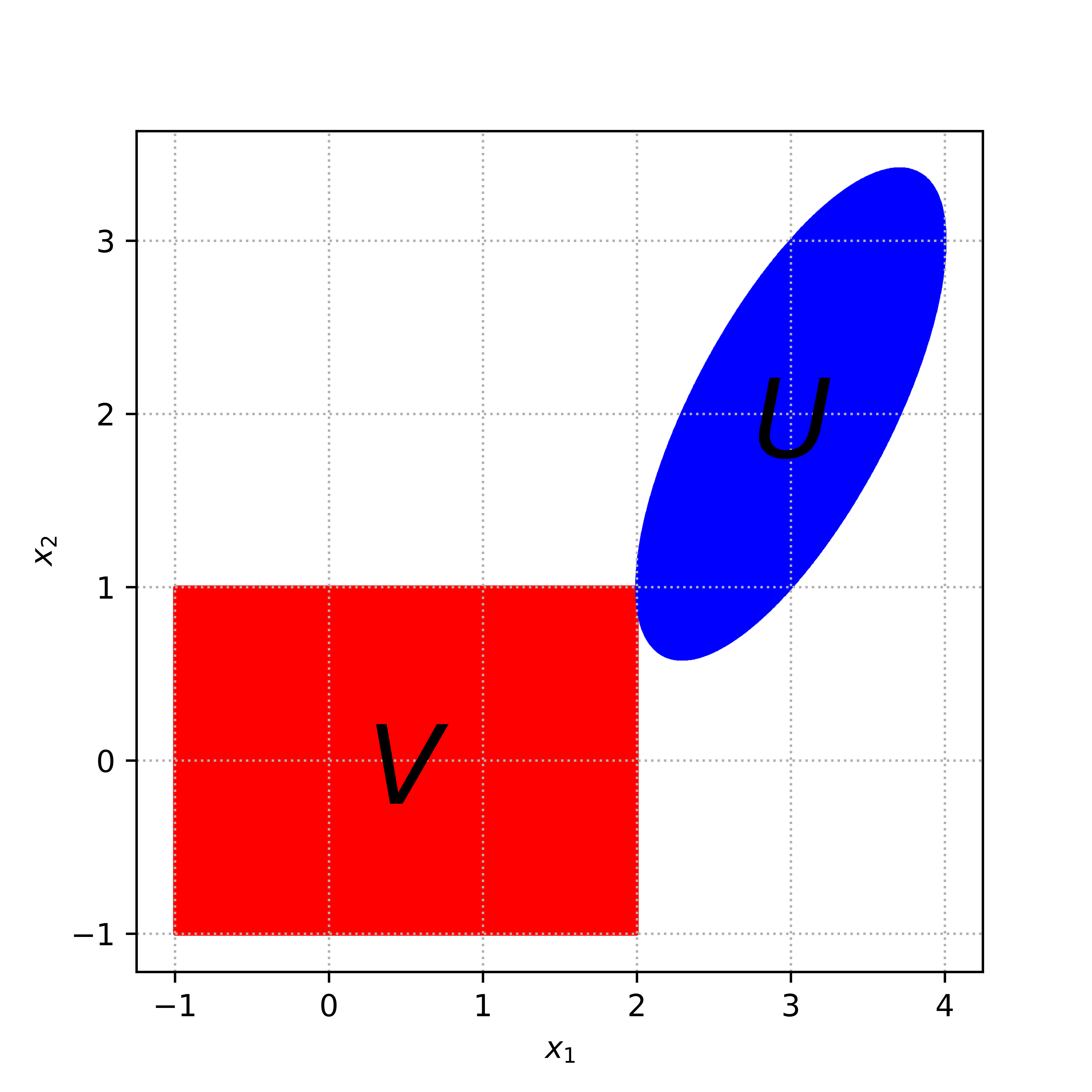
    Illustration of the problem

Accelerated methods

  1. Local Convergence of Heavy Ball Method. (10 points)

    We will work with the heavy ball method in this problem

    \tag{HB} x_{k+1} = x_k - \alpha \nabla f(x_k) + \beta (x_k - x_{k-1})

    It is known, that for the quadratics the best choice of hyperparameters is \alpha^* = \dfrac{4}{(\sqrt{L} + \sqrt{\mu})^2}, \beta^* = \dfrac{(\sqrt{L} - \sqrt{\mu})^2}{(\sqrt{L} + \sqrt{\mu})^2}, which ensures accelerated linear convergence for a strongly convex quadratic function.

    Consider the following continuously differentiable, strongly convex with parameter \mu, and smooth function with parameter L:

    f(x) = \begin{cases} \frac{25}{2}x^2, & \text{if } x < 1 \\ \frac12x^2 + 24x - 12, & \text{if } 1 \leq x < 2 \\ \frac{25}{2}x^2 - 24x + 36, & \text{if } x \geq 2 \end{cases} \quad \nabla f(x) = \begin{cases} 25x, & \text{if } x < 1 \\ x + 24, & \text{if } 1 \leq x < 2 \\ 25x - 24, & \text{if } x \geq 2 \end{cases}

    1. How to prove, that the given function is convex? Strongly convex? Smooth?

    2. Find the constants \mu and L for a given function.

    3. Plot the function value for x \in [-4, 4].

    4. Run the Heavy Ball method for the function with optimal hyperparameters \alpha^* = \dfrac{4}{(\sqrt{L} + \sqrt{\mu})^2}, \beta^* = \dfrac{(\sqrt{L} - \sqrt{\mu})^2}{(\sqrt{L} + \sqrt{\mu})^2} for quadratic function, starting from x_0 = 3.5. If you have done everything above correctly, you should receive something like

      You can use the following code for plotting:

      import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from IPython.display import HTML

# Gradient of the function
def grad_f(x):
    ...

# Heavy Ball method implementation
def heavy_ball_method(alpha, beta, x0, num_iterations):
    x = np.zeros(num_iterations + 1)
    x_prev = x0
    x_curr = x0  # Initialize x[1] same as x[0] to start the algorithm
    for i in range(num_iterations):
        x[i] = x_curr
        x_new = x_curr - alpha * grad_f(x_curr) + beta * (x_curr - x_prev)
        x_prev = x_curr
        x_curr = x_new
    x[num_iterations] = x_curr
    return x

# Parameters
L = ...
mu = ...
alpha_star = ...
beta_star = ...
x0 = ...
num_iterations = 30

# Generate the trajectory of the method
trajectory = heavy_ball_method(alpha_star, beta_star, x0, num_iterations)

# Setup the figure and axes for the animation
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(7, 3.5))
fig.suptitle("Heavy ball method with optimal hyperparameters α* β*")

# Function for updating the animation
def update(i):
    ax1.clear()
    ax2.clear()

    # Plot f(x) and trajectory
    x_vals = np.linspace(-4, 4, 100)
    f_vals = np.piecewise(x_vals, [x_vals < 1, (x_vals >= 1) & (x_vals < 2), x_vals >= 2],
                        [lambda x: 12.5 * x**2, lambda x: .5 * x**2 + 24 * x - 12, lambda x: 12.5 * x**2 - 24 * x + 36])
    ax1.plot(x_vals, f_vals, 'b-')
    ax1.plot(trajectory[:i], [12.5 * x**2 if x < 1 else .5 * x**2 + 24 * x - 12 if x < 2 else 12.5 * x**2 - 24 * x + 36 for x in trajectory[:i]], 'ro-')
    # Add vertical dashed lines at x=1 and x=2 on the left subplot
    ax1.axvline(x=1, color='navy', linestyle='--')
    ax1.axvline(x=2, color='navy', linestyle='--')

    # Plot function value from iteration
    f_trajectory = [None for x in trajectory]
    f_trajectory[:i] = [12.5 * x**2 if x < 1 else .5 * x**2 + 24 * x - 12 if x < 2 else 12.5 * x**2 - 24 * x + 36 for x in trajectory[:i]]
    ax2.plot(range(len(trajectory)), f_trajectory, 'ro-')
    ax2.set_xlim(0, len(trajectory))
    ax2.set_ylim(min(f_vals), max(f_vals))
    # Add horizontal dashed lines at f(1) and f(2) on the right subplot
    f_1 = 12.5 * 1.0**2
    f_2 = .5 * 2.**2 + 24 * 2. - 12
    ax2.axhline(y=f_1, color='navy', linestyle='--')
    ax2.axhline(y=f_2, color='navy', linestyle='--')

    # ax1.set_title("Function f(x) and Trajectory")
    ax1.set_xlabel("x")
    ax1.set_ylabel("f(x)")
    ax1.grid(linestyle=":")

    # ax2.set_title("Function Value from Iteration")
    ax2.set_xlabel("Iteration")
    ax2.set_ylabel("f(x)")
    ax2.grid(linestyle=":")

    plt.tight_layout()

# Create the animation
ani = animation.FuncAnimation(fig, update, frames=num_iterations, repeat=False, interval=100)
HTML(ani.to_jshtml())

    5. Change the starting point to x_0 = 3.4. What do you see? How could you name such a behavior of the method?

    6. Change the hyperparameter \alpha^{\text{Global}} = \frac2L, \beta^{\text{Global}} = \frac{\mu}{L} and run the method again from x_0 = 3.4. Check whether you have accelerated convergence here.

    Context: this counterexample was provided in the paper, while the global convergence of the heavy ball method for general smooth strongly convex function was introduced in another paper. Recently, it was suggested, that the heavy-ball (HB) method provably does not reach an accelerated convergence rate on smooth strongly convex problems.

  2. (20 points) In this problem we will work with accelerated methods applied to the logistic regression problem. A good visual introduction to the topic is available here.

    Logistic regression is a standard model in classification tasks. For simplicity, consider only the case of binary classification. Informally, the problem is formulated as follows: There is a training sample \{(a_i, b_i)\}_{i=1}^m, consisting of m vectors a_i \in \mathbb{R}^n (referred to as features) and corresponding numbers b_i \in \{-1, 1\} (referred to as classes or labels). The goal is to construct an algorithm b(\cdot), which for any new feature vector a automatically determines its class b(a) \in \{-1, 1\}.

    In the logistic regression model, the class determination is performed based on the sign of the linear combination of the components of the vector a with some fixed coefficients x \in \mathbb{R}^n:

    b(a) := \text{sign}(\langle a, x \rangle).

    The coefficients x are the parameters of the model and are adjusted by solving the following optimization problem:

    \tag{LogReg} \min_{x \in \mathbb{R}^n} \left( \frac{1}{m} \sum_{i=1}^m \ln(1 + \exp(-b_i \langle a_i, x \rangle)) + \frac{\lambda}{2} \|x\|^2 \right),

    where \lambda \geq 0 is the regularization coefficient (a model parameter).

    1. Will the LogReg problem be convex for \lambda = 0? What is the gradient of the objective function? Will it be strongly convex? What if you will add regularization with \lambda > 0?

    2. We will work with the real-world data for A and b: take the mushroom dataset. Be careful, you will need to predict if the mushroom is poisonous or edible. A poor model can cause death in this exercise.

      import requests
from sklearn.datasets import load_svmlight_file

# URL of the file to download
url = 'https://mipt23.fmin.xyz/files/mushrooms.txt'

# Download the file and save it locally
response = requests.get(url)
dataset = 'mushrooms.txt'

# Ensure the request was successful
if response.status_code == 200:
    with open(dataset, 'wb') as f:
        f.write(response.content)

    # Load the dataset from the downloaded file
    data = load_svmlight_file(dataset)
    A, b = data[0].toarray(), data[1]
    n, d = A.shape

    print("Data loaded successfully.")
    print(f"Number of samples: {n}, Number of features: {d}")
else:
    print(f"Failed to download the file. Status code: {response.status_code}")

    3. Divide the data into two parts: training and test. We will train the model on the A_{train}, b_{train} and measure the accuracy of the model on the A_{test}, b_{test}.

      from sklearn.model_selection import train_test_split
# Split the data into training and test sets
A_train, A_test, b_train, b_test = train_test_split(A, b, test_size=0.2, random_state=214)

    4. For the training part A_{train}, b_{train}, estimate the constants \mu, L of the training/optimization problem. Use the same small value \lambda for all experiments

    5. Using gradient descent with the step \frac{1}{L}, train a model. Plot: accuracy versus iteration number.

      \tag{HB} x_{k+1} = x_k - \alpha \nabla f(x_k) + \beta (x_k - x_{k-1})

      Fix a step \alpha = \frac{1}{L} and search for different values of the momentum \beta from -1 to 1. Choose your own convergence criterion and plot convergence for several values of momentum on the same graph. Is the convergence always monotonic?

    6. For the best value of momentum \beta, plot the dependence of the model accuracy on the test sample on the running time of the method. Add to the same graph the convergence of gradient descent with step \frac{1}{L}. Draw a conclusion. Ensure, that you use the same value of \lambda for both methods.

    7. Solve the logistic regression problem using the Nesterov method.

      \tag{NAG} x_{k+1} = x_k - \alpha \nabla f(x_k + \beta (x_k - x_{k-1})) + \beta (x_k - x_{k-1})

      Fix a step \frac{1}{L} and search for different values of momentum \beta from -1 to 1. Check also the momentum values equal to \frac{k}{k+3}, \frac{k}{k+2}, \frac{k}{k+1} (k is the number of iterations), and if you are solving a strongly convex problem, also \frac{\sqrt{L} - \sqrt{\mu}}{\sqrt{L} + \sqrt{\mu}}. Plot the convergence of the method as a function of the number of iterations (choose the convergence criterion yourself) for different values of the momentum. Is the convergence always monotonic?

    8. For the best value of momentum \beta, plot the dependence of the model accuracy on the test sample on the running time of the method. Add this graph to the graphs for the heavy ball and gradient descent from the previous steps. Make a conclusion.

    9. Now we drop the estimated value of L and will try to do it adaptively. Let us make the selection of the constant L adaptive.

      f(y) \leq f(x^k) + \langle \nabla f(x^k), y - x^k \rangle + \frac{L}{2}\|x^k - y\|_2^2

      In particular, the procedure might work:

      def backtracking_L(f, grad, x, h, L0, rho, maxiter=100):
    L = L0
    fx = f(x)
    gradx = grad(x)
    iter = 0
    while iter < maxiter :
        y = x - 1 / L * h
        if f(y) <= fx - 1 / L gradx.dot(h) + 1 / (2 * L) h.dot(h):
            break
        else:
            L = L * rho

        iter += 1
    return L

      What should h be taken as? Should \rho be greater or less than 1? Should L_0 be taken as large or small? Draw a similar figure as it was in the previous step for L computed adaptively (6 lines - GD, HB, NAG, GD adaptive L, HB adaptive L, NAG adaptive L)

Gradient methods for conditional problems

  1. 💍 Hobbit village (Gradient descent + Newton method + Gradient descent in conditional optimization) (20 points)

    %matplotlib inline
import numpy as np
from matplotlib import pyplot as plt
import matplotlib as mpl
import seaborn as sns
import copy
sns.set()

    Below one can find function plotting the village

    def plot_village(coordinates, l=1):
    # Checking, that all the coordinates are less than l
    assert (coordinates <= l).all(), 'All the houses should be in a village'

    # Draw horizontal line
    plt.hlines(0, 0, l)
    plt.xlim(0, l)
    plt.ylim(-0.5, 0.5)

    # Draw house points
    y = np.zeros(np.shape(coordinates))
    plt.title('The Hobbit Village')
    plt.plot(coordinates,y,'o',ms = 10)
    plt.axis('off')
    plt.xlabel('Coordinates')
    fig = plt.gcf()
    fig.set_size_inches(15, 1)
    plt.show()

N = 25
l = 1
x = np.random.rand(N)*l

plot_village(x, l)

    The inhabitants of a one-dimensional village want to connect to the Internet, so they need a central service station from which a cable will stretch to all the houses in the village. Let the price of the cable to be pulled from the station to each house independently be determined by some function p(d). Then it is clear that the village will have to pay the following amount for access to the World Wide Web: P(w, x) = \sum\limits_{i=1}^N p(d_i) = \sum\limits_{i=1}^N p(|w - x_i|) w - station location, x_i - location of i house.

    1. Write analytical solution w^* for minimization P(w,x), if p(d) = d^2

    2. Write loss function P(w,x)

      def P(w, x):
    return ((x-w)**2).sum()
    # pass

    3. Plot loss function on the range (0, l):

      ### YOUR CODE
ws = np.linspace(0, 1)
plt.plot(ws, [P(w, x) for w in ws])

    4. Write gradient of loss function

      def dP(w, x):
    return (2*(w-x)).sum()

    5. Plot gradient of loss function on the range (0,l). Which point on the graph is of particular interest? Why?

      ### YOUR CODE
ws = np.linspace(0, 1)
plt.plot(ws, [dP(w, x) for w in ws])

    6. Write function gradient_descent, which returns w_k after a fixed number of steps.

      w_{k+1} = w_k - \mu \nabla P(w_k) 

      w0 = np.random.rand()*10

def gradient_descent(x, dP, w0, mu, Nsteps):
    pass

    7. Modify gradient_descent to return the whole optimization trajectory. Plot loss function trajectory for the following learning rates \mu = 0.0001, 0.001, 0.01, 0.1.
      Draw conclusions.

      def gradient_descent(x, dP, w0, mu, Nsteps):
return trajectory

    8. The village decided to lay cable using new technology. That’s why the price of the cable changed to:

      p(d) = |d|

      Write new function P, dP. Plot graphs for various x and w.

      def P(w, x):
    pass

def dP(w, x):
    pass

    9. Write new analytical solytion w^*

    10. Plot loss trajectory for converging gradient descent for the new p(d).

    11. After several years, the government propose to destroy the first station but choose locations for two new stations. In this conditions cost of connecting all house calculated by new formula:

      P(w_1, w_2, x) = \sum\limits_{i=1}^N p(d_i) = \sum\limits_{i=1}^N p\left(\min\left(\left|w_1 - x_i\right|, \left|w_2 - x_i\right|\right)\right)

      Write new P, dP.

      def P(w1, w2, x):
    pass

def dP(w1, w2, x):
    pass

    12. Plot P(w_1, w_2), \nabla P(w_1, w_2) for different number of houses N. Comment on what happens as you increase N.

    13. Write new gradient_descent, which returns the entire optimization trajectory (w_k) after a fixed number of steps and draws the process on the graphs P and \nabla P that were above. To ease visualization try to use ax.quiver

      def gradient_descent(x, dP, w0, mu, Nsteps):
    pass

    14. Construction is almost underway, but new safety regulations do not allow stations to be on the distance more than 1/2:

      \left|w_1 - w_2\right| \leq \dfrac{l}{2}

      Plot our feasible set. Is it convex?

    15. Write projected_SGD, which returns the entire optimization trajectory (w_k) after a fixed number of steps and draws the process on the graphs P and \nabla P that were above.

      The projected gradient descent method consists in making a gradient step and then checking if the obtained point belongs to the feasible set. If it belongs to the target set, the algorithm continues, otherwise a projection to the feasible set is made.

      def projected_SGD(x, dP_sigma, w0, mu, Nsteps, p=0.4):
    pass

def projection(w):
    pass

    16. We have same loss function

      P(w, x) = \sum\limits_{i=1}^N p(d_i) = \sum\limits_{i=1}^N p(|w - x_i|),

      where p(d) = d^2

      Write functions P, dP, ddP. ddP has to return hessian of loss function

      def P(w, x):
    ### YOUR CODE
    return

def dP(w, x):
    ### YOUR CODE
    return 

def ddP(w, x):
    ### YOUR CODE
    return

    17. Plot ddP on the range (0,l)

    18. Write function newton_descent, which return all optimization trajectory. Update rule:

      w_{i+1} = w_{i} - \nabla^{2} P\left(w_{i}\right)^{-1} \nabla P\left(w_{i}\right) 

      def newton_descent(x, dP, ddP, w0, Nsteps):
    return trajectory

    19. Write function multi_newton, which solve 2D task:

      P(w_1, w_2, x) = \sum\limits_{i=1}^N p(d_i) = \sum\limits_{i=1}^N p\left(\min\left(\left|w_1 - x_i\right|, \left|w_2 - x_i\right|\right)\right)

      with p(d) = d^3 using Newton method and return optimization trajectory. Compare results with gradient descent.

      def P(w1, w2, x):
    ### YOUR CODE
    return 

def dP(w1, w2, x):
    ### YOUR CODE
    return 

def ddP(w1, w2, x):
    ### YOUR CODE
    return 

def multi_newton(x, dP, ddP, w0, Nsteps):
    ### YOUR CODE
    return trajectory

  2. 🐺 Frank - Wolfe vs Projected gradient descent (10 points)

    Consider the following simple quadratic optimization problem

    f(w) = \frac12 \langle Ax, x \rangle - \langle b, x \rangle \to \min\limits_{x \in \mathbb{R}^n; \; 1^\top x = 1, \; x \succeq 0}

    1. Generate and solve this problem numerically with CVXPY. Calculate optimal solution x_optimal

      import jax
from jax import numpy as jnp
from jax import random
from jax import grad

def generate_problem(n, mu=0, L = 10):
    RNG = random.PRNGKey(0)

    U = random.normal(RNG, (n, n))
    Q, _ = jnp.linalg.qr(U)
    Lambda = jnp.diag(jnp.linspace(mu, L, n, endpoint=True))
    A = Q @ Lambda @ Q.T

    RNG, _ = random.split(RNG)
    b = random.normal(RNG, (n, 1))

    def f(x, A=A, b=b):
        return 1/2 * x.T @ A @ x - b.T @ x

    grad_f = grad(f)

    RNG, _ = random.split(RNG)
    x_0 = jnp.zeros(n)
    idx = random.randint(RNG, (1,), 0, n)
    x_0 = x_0.at[idx].set(1.0)

    return f, grad_f, A, b, x_0

def compute optimal(A, b):
    ### ======
    ### YOUR CODE HERE
    ### ======
    return x_optimal

    2. In this problem you will consider 2 algorithms for solving this problem (Frank - Wolfe and Projected Gradient Descent). Let’s start with PGD. Write down the function, that calculates Euclidian projection on the simplex:

      def projection(y):
    ### ======
    ### YOUR CODE HERE
    ### ======
    return x

    3. Then, write the PGD method, that returns a trajectory list of iterations+1 points x_0, x_1, \ldots x_k and time_trajectory list for a cumulative time spent after each iteration :

      def PGD(A, b, x_0, iterations):
    return trajectory, time_trajectory

    4. Write down the FW method, that returns a trajectory list of iterations+1 points x_0, x_1, \ldots x_k and time_trajectory list for a cumulative time spent after each iteration :

      def FW(A, b, x_0, iterations):
    return trajectory, time_trajectory

    5. Generate a convex problem (\mu=0, L=10) and compare the methods starting from the same x_0. For this reason plot 2 graphs - f(x_k) - f^* from iteration counter and time spent for it.

    6. Generate a strongly convex problem (\mu=1, L=10) and compare the methods starting from the same x_0. For this reason plot 2 graphs - f(x_k) - f^* from iteration counter and time spent for it.

Conjugate gradients

  1. Randomized Preconditioners for Conjugate Gradient Methods. (20 points)

    Linear least squares

    In this task, we explore the use of some randomization methods for solving overdetermined least-squares problems, focusing on conjugate gradient methods. Let \hat{A} \in \mathbb{R}^{m \times n} be a matrix (we assume that m \gg n) and b \in \mathbb{R}^m, we aim to minimize

    f(x) = \frac{1}{2} \|\hat{A}x - b\|^2_2 = \frac{1}{2} \sum_{i=1}^m (\hat{a}_i^T x - b_i)^2,

    where the \hat{a}_i \in \mathbb{R}^n denote the rows of \hat{A}.

    Preconditioners

    We know, that the convergence bound of the CG applied for the problem depends on the condition number of the matrix. Note, that for the problem above we have the matrix \hat{A}^T \hat{A} and the condition number is squared after this operation (\kappa (X^T X) = \kappa^2 \left(X \right)). That is the reason, why we typically need to use preconditioners (read 12. for more details) with CG.

    The general idea of using preconditioners implies switchwing from solving Ax = b to MAx = Mb with hope, that \kappa \left( MA\right) \ll \kappa \left( A\right) or eigenvalues of MA are better clustered than those of A (note, that matrix A here is for the general case, here we have \hat{A}^T\hat{A} instead).

    This idea can also be viewed as coordinate change x = T \hat{x}, \; \hat{x} = T^{-1}x, which leads to the problem T^T A T \hat{x} = T^Tb. Note, that the spectrum of T^TAT is the same as the spectrum of MA.

    The best choice of M is A^{-1}, because \kappa (A^{-1} A) = \kappa (I) = 1. However, if we know A^{-1}, the original problem is already solved, that is why we need to find some trade-off between enhanced convergence, and extra cost of working with M. The goal is to find M that is cheap to multiply, and approximate inverse of A (or at least has a more clustered spectrum than A).

    Note, that for the linear least squares problem the matrix of quadratic form is A = \hat{A}^T\hat{A}. Below you can find Vanilla CG algorithm (on the left) and preconditioned CG algorithm (on the right):

    \begin{aligned} & \mathbf{r}_0 := \mathbf{b} - \mathbf{A x}_0 \\ & \hbox{if } \mathbf{r}_{0} \text{ is sufficiently small, then return } \mathbf{x}_{0} \text{ as the result}\\ & \mathbf{d}_0 := \mathbf{r}_0 \\ & k := 0 \\ & \text{repeat} \\ & \qquad \alpha_k := \frac{\mathbf{r}_k^\mathsf{T} \mathbf{r}_k}{\mathbf{d}_k^\mathsf{T} \mathbf{A d}_k} \\ & \qquad \mathbf{x}_{k+1} := \mathbf{x}_k + \alpha_k \mathbf{d}_k \\ & \qquad \mathbf{r}_{k+1} := \mathbf{r}_k - \alpha_k \mathbf{A d}_k \\ & \qquad \hbox{if } \mathbf{r}_{k+1} \text{ is sufficiently small, then exit loop} \\ & \qquad \beta_k := \frac{\mathbf{r}_{k+1}^\mathsf{T} \mathbf{r}_{k+1}}{\mathbf{r}_k^\mathsf{T} \mathbf{r}_k} \\ & \qquad \mathbf{d}_{k+1} := \mathbf{r}_{k+1} + \beta_k \mathbf{d}_k \\ & \qquad k := k + 1 \\ & \text{end repeat} \\ & \text{return } \mathbf{x}_{k+1} \text{ as the result} \end{aligned} \qquad \begin{aligned} & \mathbf{r}_0 := \mathbf{b} - \mathbf{A x}_0 \\ & \text{if } \mathbf{r}_0 \text{ is sufficiently small, then return } \mathbf{x}_0 \text{ as the result} \\ & \mathbf{z}_0 := \mathbf{M}^{-1} \mathbf{r}_0 \\ & \mathbf{d}_0 := \mathbf{z}_0 \\ & k := 0 \\ & \text{repeat} \\ & \qquad \alpha_k := \frac{\mathbf{r}_k^\mathsf{T} \mathbf{z}_k}{\mathbf{d}_k^\mathsf{T} \mathbf{A d}_k} \\ & \qquad \mathbf{x}_{k+1} := \mathbf{x}_k + \alpha_k \mathbf{d}_k \\ & \qquad \mathbf{r}_{k+1} := \mathbf{r}_k - \alpha_k \mathbf{A d}_k \\ & \qquad \text{if } \mathbf{r}_{k+1} \text{ is sufficiently small, then exit loop} \\ & \qquad \mathbf{z}_{k+1} := \mathbf{M}^{-1} \mathbf{r}_{k+1} \\ & \qquad \beta_k := \frac{\mathbf{r}_{k+1}^\mathsf{T} \mathbf{z}_{k+1}}{\mathbf{r}_k^\mathsf{T} \mathbf{z}_k} \\ & \qquad \mathbf{d}_{k+1} := \mathbf{z}_{k+1} + \beta_k \mathbf{d}_k \\ & \qquad k := k + 1 \\ & \text{end repeat} \\ & \text{return } \mathbf{x}_{k+1} \text{ as the result} \end{aligned}

    Hadamard matrix

    Given m \in \{2^i, i = 1, 2, \ldots\}, the (unnormalized) Hadamard matrix of order m is defined recursively as

    H_2 = \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}, \quad \text{and} \quad H_m = \begin{bmatrix} H_{m/2} & H_{m/2} \\ H_{m/2} & -H_{m/2} \end{bmatrix}.

    The associated normalized Hadamard matrix is given by H^{(\text{norm})}_m = \frac{1}{\sqrt{m}} H_m, which evidently satisfies H^{(\text{norm})T}_m H^{(\text{norm})}_m = I_{m \times m}. Moreover, via a recursive algorithm, it is possible to compute matvec H_m x in time O(m \log m), which is much faster than m^2 for a general matrix.

    To solve the least squares minimization problem using conjugate gradients, we must solve \hat{A}^T \hat{A} x = \hat{A}^T b. Using a preconditioner M such that M \approx A^{-1} can give substantial speedup in computing solutions to large problems.

    Consider the following scheme to generate a randomized preconditioner, assuming that m = 2^i for some i:

    1. Let S = \text{diag}(S_{11}, \ldots, S_{mm}), where S_{jj} are random \{-1,+1\} signs

    2. Let p \in \mathbb{Z}^+ be a small positive integer, say 20 for this problem.

    3. Let R \in \{0, 1\}^{n+p \times m} be a row selection matrix, meaning that each row of R has only 1 non-zero entry, chosen uniformly at random. (The location of these non-zero columns is distinct.)

      import jax.numpy as jnp
from jax import random

def create_row_selection_matrix_jax(m, n, p, key):
    # m is the number of columns in the original matrix A
    # n+p is the number of rows in the row selection matrix R
    # key is a PRNGKey needed for randomness in JAX
    inds = random.permutation(key, m)[:n+p]  # Generate a random permutation and select the first n+p indices
    R = jnp.zeros((n+p, m), dtype=jnp.int32)  # Create a zero matrix of shape (n+p, m)
    R = R.at[np.arange(n+p), inds].set(1)     # Use JAX's indexed update to set the entries corresponding to inds to 1
    return R

    4. Define \Phi = R H^{(\text{norm})}_m S \in \mathbb{R}^{n+p \times m}

    We then define the matrix M via its inverse M^{-1} = \hat{A}^T \Phi^T \Phi \hat{A} \in \mathbb{R}^{n \times n}.

    Questions

    1. (2 point) How many FLOPs (floating point operations, i.e. multiplication and additions) are required to compute the matrices M^{-1} and M, respectively, assuming that you can compute the matrix-vector product H_mv in time m \log m for any vector v \in \mathbb{R}^m?

    2. (2 point) How many FLOPs are required to naively compute \hat{A}^T \hat{A}, assuming \hat{A} is dense (using standard matrix algorithms)?

    3. (2 point) How many FLOPs are required to compute \hat{A}^T \hat{A} v for a vector v \in \mathbb{R}^n by first computing u = \hat{A}v and then computing \hat{A}^T u?

    4. (4 poins) Suppose that conjugate gradients runs for k iterations. Using the preconditioned conjugate gradient algorithm with M = (\hat{A}^T \Phi^T \Phi \hat{A})^{-1}, how many total floating point operations have been performed? How many would be required to directly solve \hat{A}^T \hat{A} x = \hat{A}^T b? How large must k be to make the conjugate gradient method slower?

    5. (10 points) Implement the conjugate gradient algorithm for solving the positive definite linear system \hat{A}^T \hat{A} x = \hat{A}^T b both with and without the preconditioner M. To generate data for your problem, set m = 2^{12} and n = 400, then generate the matrix A and the vector b. For simplicity in implementation, you may directly pass \hat{A}^T \hat{A} and \hat{A}^T b into your conjugate gradient solver, as we only wish to explore how the methods work.

    import numpy as np
from scipy.sparse import diags

m = 2**12  # 4096
n = 400
# Create a linear space of values from 0.001 to 100
values = np.linspace(0.001, 100, n)
# Generate the matrix A
A = np.random.randn(m, n) * diags(values).toarray()
b = np.random.randn(m, 1)

    Plot the norm of the residual r_k = \hat{A}^T b - \hat{A}^T \hat{A} x_k (relative to \|\hat{A}^T b\|_2) as a function of iteration k for each of your conjugate gradient procedures. Additionally, compute and print the condition numbers \kappa(\hat{A}^T \hat{A}) and \kappa(M^{1/2} \hat{A}^T \hat{A} M^{1/2}).

Newton and quasinewton methods

  1. 😱 Newton convergence issue (10 points)

    Consider the following function:

    f(x,y) = \dfrac{x^4}{4} - x^2 + 2x + (y-1)^2

    And the starting point is x_0 = (0,2)^\top. How does Newton’s method behave when started from this point? How can this be explained? How does the gradient descent with fixed step \alpha = 0.01 and the steepest descent method behave under the same conditions? (It is not necessary to show numerical simulations in this problem).

  2. Hessian-Free Newton method (20 points) In this exercise, we’ll explore the optimization of a binary logistic regression problem using various methods. Don’t worry about the size of the problem description, first 5 bullets out of 7 could be done pretty quickly. In this problem you should start with this colab notebook

    Given a dataset with n observations, where each observation consists of a feature vector x_i and an associated binary target variable y_i \in \{0,1\}, the logistic regression model predicts the probability that y_i = 1 given x_i using the logistic function. The loss function to be minimized is the negative log-likelihood of the observed outcomes under this model, summed across all observations. It has a high value when the model outputs differ significantly from the data y.

    The binary cross-entropy loss function for a single observation (x_i, y_i) is given by: \text{Loss}(w; x_i, y_i) = -\left[ y_i \log(p(y_i=1 | x_i; w)) + (1-y_i) \log(1-p(y_i=1 | x_i; w)) \right]

    Here, p(y=1 | x;w) is defined as: p(y=1 | x;w) = \frac{1}{1 + e^{-w^T x}}

    To define the total loss over the dataset, we sum up the individual losses: f(w) = -\sum_{i=1}^n \left[ y_i \log(p(y_i=1 | x_i; w)) + (1-y_i) \log(1-p(y_i=1 | x_i; w)) \right]

    Therefore, the optimization problem in logistic regression is: \min_w f(w) = \min_w -\sum_{i=1}^n \left[ y_i \log\left(p\left(y_i=1 | x_i; w\right)\right) + \left(1-y_i\right) \log\left(1-p(y_i=1 | x_i; w)\right) \right]

    This is a convex optimization problem and can be solved using gradient-based methods such as gradient descent, Newton’s method, or more sophisticated optimization algorithms often available in machine learning libraries. However, it is the problem is often together with l_2 regularization:

    \min_w f(w) = \min_w -\sum_{i=1}^n \left[ y_i \log\left(p\left(y_i=1 | x_i; w\right)\right) + \left(1-y_i\right) \log\left(1-p(y_i=1 | x_i; w)\right) \right] + \frac{\mu}{2} \|w\|_2^2

    1. (2 points) Firstly, we address the optimization with Gradient Descent (GD) in a strongly convex setting, with \mu = 1. Use a constant learning rate \alpha. Run the gradient descent algorithm. Report the highest learning rate that ensures convergence of the algorithm. Plot the convergence graph in terms of both domain (parameter values) and function value (loss). Describe the type of convergence observed.

      params = {
    "mu": 1,
    "m": 1000,
    "n": 100,
    "methods": [
        {
            "method": "GD",
            "learning_rate": 3e-2,
            "iterations": 550,
        },
    ]
}

results, params = run_experiments(params)

    2. (2 points) Run Newton’s method under the same conditions, using the second derivatives to guide the optimization. Describe and analyze the convergence properties observed.

      params = {
    "mu": 1,
    "m": 1000,
    "n": 100,
    "methods": [
        {
            "method": "GD",
            "learning_rate": 3e-2,
            "iterations": 550,
        },
        {
            "method": "Newton",
            "iterations": 20,
        },
    ]
}

results, params = run_experiments(params)

    3. (2 points) In cases where Newton’s method may converge too rapidly or overshoot, a damped version can be more stable. Run the damped Newton method. Adjust the damping factor as a learning rate. Report the highest learning rate ensuring stability and convergence. Plot the convergence graph.

      params = {
    "mu": 1,
    "m": 1000,
    "n": 100,
    "methods": [
        {
            "method": "GD",
            "learning_rate": 3e-2,
            "iterations": 550,
        },
        {
            "method": "Newton",
            "iterations": 20,
        },
        {
            "method": "Newton",
            "learning_rate": 5e-1,
            "iterations": 50,
        },
    ]
}

results, params = run_experiments(params)

    4. (2 points) Now turn off the regularization by setting \mu=0. Try to find the largest learning rate, which ensures convergence of the Gradient Descent. Use a constant learning rate \alpha. Run the gradient descent algorithm. Report the highest learning rate that ensures convergence of the algorithm. Plot the convergence graph in terms of both domain (parameter values) and function value (loss). Describe the type of convergence observed. How can you describe an idea to run this method for the problem to reach tight primal gap f(x_k) - f^* \approx 10^{-2} or 10^{-3}, 10^{-4}?

      params = {
    "mu": 0,
    "m": 1000,
    "n": 100,
    "methods": [
        {
            "method": "GD",
            "learning_rate": 3e-2,
            "iterations": 200,
        },
        {
            "method": "GD",
            "learning_rate": 7e-2,
            "iterations": 200,
        },
    ]
}

results, params = run_experiments(params)

    5. (2 points) What can you say about Newton’s method convergence in the same setting \mu=0? Try several learning rates smaller, than 1 for the damped Newton method. Does it work? Write your conclusions about the second-order method convergence for a binary logistic regression problem.

    6. (5 points) Now switch back to the strongly convex setting \mu=1. To avoid directly computing the Hessian matrix in Newton’s method, use the Conjugate Gradient (CG) method to solve the linear system in the Newton step. Develop the newton_method_cg function, which computes the Newton step using CG to solve the system \nabla^2 f(x_k) d_k = - \nabla f(x_k), \; x_{k+1} = x_k - \alpha d_k defined by the Hessian. You have to use jax.scipy.sparse.linalg.cg function here. So, firstly compute the hessian as it was done in the code, then put it into this linear solver. Compare its performance in terms of computational efficiency and convergence rate to the standard Newton method.

    7. (5 points) Finally, implement a Hessian-free version of Newton’s method (HFN) which utilizes Hessian-vector products derived via automatic differentiation. Note, that jax.scipy.sparse.linalg.cg function can take the matvec function, which directly produces the multiplication of any input vector x. Implement the HFN method without explicitly forming or storing the Hessian matrix in function newton_method_hfn. Use autograd to compute Hessian-vector products as it is described here. Compare this method’s time complexity and memory requirements against previous implementations.

Proximal Gradient Method

  1. [20 points] Proximal Method for Sparse Softmax Regression Softmax regression, also known as multinomial logistic regression, is a generalization of logistic regression to multiple classes. It is used to model categorical outcome variables where each category is mutually exclusive. The softmax function transforms any input vector to the probability-like vector as follows:

    P(y = j | x; W) = \frac{e^{W_j^T x}}{\sum\limits_{i=1}^{c} e^{W_i^T x}}

    Scheme of softmax regression

    where x is the input vector, W is the weight matrix, c is the number of classes, and P(y = j | x; W) is the probability that the input x belongs to class j.

    The optimization problem for softmax regression is to minimize the negative log-likelihood:

    \min_{W \in \mathbb{R}^{c \times d}} -\sum_{i=1}^{N} \log P(y_i | x_i; W) + \lambda \| W \|_1

    where N is the number of training examples, \lambda is the regularization parameter, and \| W \|_1 is the L1 norm of the weight matrix, which promotes sparsity in the solution. I suggest you to vectorize matrix and add 1-vector norm.

    We will solve the sparse softmax regression problem using the subgradient method and the proximal gradient method, both incorporating L1 regularization. The proximal gradient method is particularly useful for optimization problems involving non-smooth regularizers like the L1 norm. We will use 3 class classification problem of Predicting Students’ Dropout and Academic Success. In this problem you should start with this colab notebook

    1. [4 points] Write down exact formulation of subgradient method and proximal gradient method here (you can not use any optimization problems in this formulation).
    2. [6 points] Choose \lambda = 0. Solve the softmax regression problem using subgradient descent and proximal gradient descent. Find the highest learning (individually), acceptable for both methods to converge. Report convergence curves and report final sparsity of both methods. Draw you conclusions.
    3. [10 points] Solve non-smooth problem and fill the following table. For each value of \lambda provide convergence curves.

    Report the number of iterations needed to reach specified primal gaps for each method. Present the results in the following markdown table:

    Method Learning Rate (\eta) Tolerance (\epsilon) Number of Iterations Comment(if any) Final Sparsity of the solution \lambda Final test accuracy
    Subgradient Descent 10^{-1} 1e-2
    Subgradient Descent 10^{-2} 1e-2
    Subgradient Descent 10^{-3} 1e-2
    Subgradient Descent 10^{-4} 1e-2
    Subgradient Descent 10^{-5} 1e-2
    Proximal Gradient Descent 10^{-1} 1e-2
    Proximal Gradient Descent 10^{-2} 1e-2
    Proximal Gradient Descent 10^{-3} 1e-2
    Proximal Gradient Descent 10^{-4} 1e-2
    Proximal Gradient Descent 10^{-5} 1e-2
    Subgradient Descent 10^{-2} 1e-3
    Proximal Gradient Descent 10^{-2} 1e-3
    Subgradient Descent 10^{-2} 1e-1
    Proximal Gradient Descent 10^{-2} 1e-1
    Subgradient Descent 10^{-2} 1
    Proximal Gradient Descent 10^{-2} 1

Stochastic gradient methods

  1. Variance reduction for stochastic gradient methods for neural networks. [20 points]

    Open colab notebook. Implement SAG and SVRG method. Consider Linear least squares problem with the following setup

    params = {
    "mu": 0,
    "m": 50,
    "n": 100,
    "methods": [
        {
            "method": "SGD",
            "learning_rate": 1e-2,
            "batch_size": 2,
            "iterations": 1000,
        },
        {
            "method": "SGD",
            "learning_rate": 1e-2,
            "batch_size": 50,
            "iterations": 1000,
        },
        {
            "method": "SAG",
            "learning_rate": 1e-2,
            "batch_size": 2,
            "iterations": 1000,
        },
        {
            "method": "SVRG",
            "learning_rate": 1e-2,
            "epoch_length": 2,
            "batch_size": 2,
            "iterations": 1000,
        },
    ]
}

results = run_experiments(params)

    Then, consider strongly convex case with:

    params = {
    "mu": 1e-1,
    "m": 50,
    "n": 100,
    "methods": [
        {
            "method": "SGD",
            "learning_rate": 1e-2,
            "batch_size": 2,
            "iterations": 2000,
        },
        {
            "method": "SGD",
            "learning_rate": 1e-2,
            "batch_size": 50,
            "iterations": 2000,
        },
        {
            "method": "SAG",
            "learning_rate": 1e-2,
            "batch_size": 2,
            "iterations": 2000,
        },
        {
            "method": "SVRG",
            "learning_rate": 1e-2,
            "epoch_length": 2,
            "batch_size": 2,
            "iterations": 2000,
        },
    ]
}

    And for the convex binary logistic regression:

    params = {
    "mu": 0,
    "m": 100,
    "n": 200,
    "methods": [
        {
            "method": "SGD",
            "learning_rate": 1e-2,
            "batch_size": 2,
            "iterations": 2000,
        },
        {
            "method": "SAG",
            "learning_rate": 1e-2,
            "batch_size": 2,
            "iterations": 2000,
        },
        {
            "method": "SVRG",
            "learning_rate": 1e-2,
            "epoch_length": 3,
            "batch_size": 2,
            "iterations": 2000,
        },
        {
            "method": "SGD",
            "learning_rate": 1e-2,
            "batch_size": 100,
            "iterations": 2000,
        },
    ]
}

    and strongly convex case

    params = {
    "mu": 1e-1,
    "m": 100,
    "n": 200,
    "methods": [
        {
            "method": "SGD",
            "learning_rate": 2e-2,
            "batch_size": 2,
            "iterations": 3000,
        },
        {
            "method": "SAG",
            "learning_rate": 2e-2,
            "batch_size": 2,
            "iterations": 3000,
        },
        {
            "method": "SVRG",
            "learning_rate": 2e-2,
            "epoch_length": 3,
            "batch_size": 2,
            "iterations": 3000,
        },
        {
            "method": "SGD",
            "learning_rate": 2e-2,
            "batch_size": 100,
            "iterations": 3000,
        },
    ]
}

    Describe the obtained convergence and compare methods.

Big models

  1. Fit the largest model you can on a single GPU. [20 points]

    In this assignment, you will train a language model (LM) using the TinyStories dataset, focusing on optimizing model performance within the constraints of Google Colab’s hardware. For the sake of speed, we will do it on the part of the dataset.

    Tiny Stories Once upon a time, there was a little car named Beep. Beep loved to go fast and play in the sun. Beep was a healthy car because he always had good fuel....

    Your objective is to maximize the size of the model without exceeding the available computational resources (~ 16GB VRAM). You could start with the Hugging Face Transformers library and experiment with various memory optimization techniques, such as (but not limited to):

     * Different batch size
 * Different optimizer
 * Gradient accumulation
 * Activation checkpointing
 * CPU offloading
 * 8bit optimizers

    You have a baseline of training gpt-2 model prepared at the following colab notebook. You can easily switch it to opt-350m, opt-1.3b, gpt2 etc. You can find a great beginner-level guide on the topic here.

    GPT-2 generation A long time ago in a galaxy far far away... a little girl named Lily was playing in the garden. She was so excited! She wanted to explore the garden and see what was around her. Suddenly, she heard a loud noise. Lily looked up and saw a big, hairy creature. Lily was so excited! She ran to the creature and grabbed it by the arm. The creature was so big and hairy that Lily couldn't help but laugh.

    You have to fill this table with your description/observations.

    Setup # of parameters GPU peak memory, MB Final eval loss Batch Size Time to run 5 epochs, s Generation example Comment
    Baseline (OPT-125M) 125 M 9044 1.928 8 442.34 A long time ago in a galaxy far far away... there was a little girl named Lily. She was three years old and loved to explore. One day, she decided to go for a walk in the park. Lily was so excited to go for a walk. She asked her mom, "What do you want to do?" Her mom smiled and said, "I want to explore the galaxy." Lily was so excited to explore the galaxy.
    Baseline (GPT2-S) 124 M 13016 2.001 8 487.75 A long time ago in a galaxy far far away... a little girl named Lily was playing in the garden. She was so excited! She wanted to explore the garden and see what was around her. Suddenly, she heard a loud noise. Lily looked up and saw a big, hairy creature. Lily was so excited! She ran to the creature and grabbed it by the arm. The creature was so big and hairy that Lily couldn't help but laugh. The generation seems more interesting, despite the fact, that eval loss is higher.

    For each unique trick for memory optimization, you will get 4 points (maximum 20 points). A combination of tricks is not counted as a unique trick, but will, probably, be necessary to train big models. The maximum grade is bounded with the size of the trained model: * If the model size you train is <= 125M - you can get a maximum of 8 points. * If the model size you train is 126M <= 350M - you can get a maximum of 12 points. * If the model size you train is 350M <= 1B - you can get a maximum of 16 points. * If you fit 1B model or more - you can get a maximum 20 points.